常见排序算法实现
常见排序算法实现
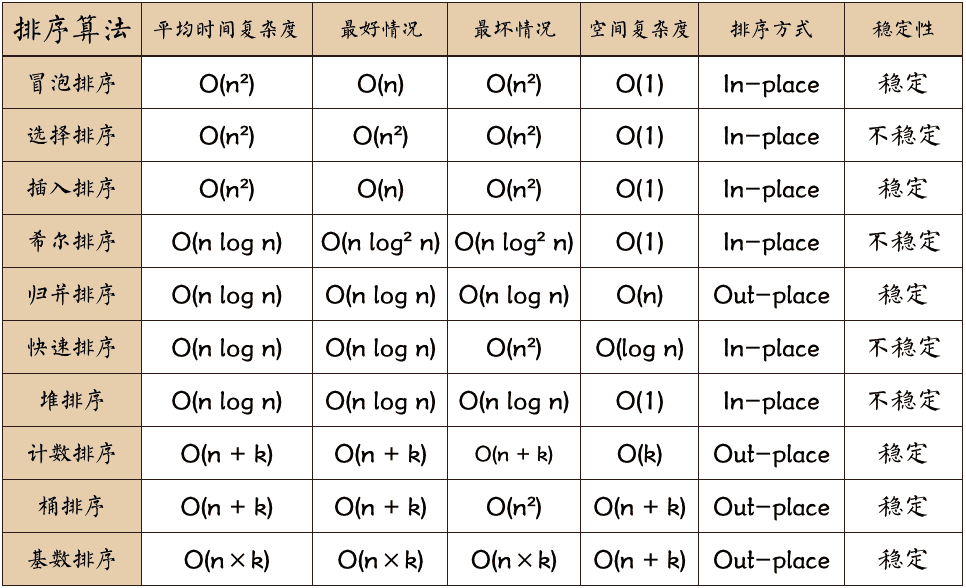
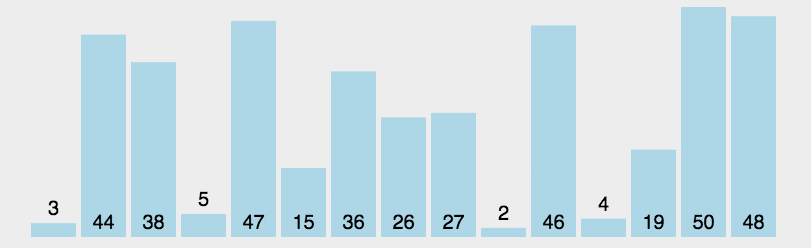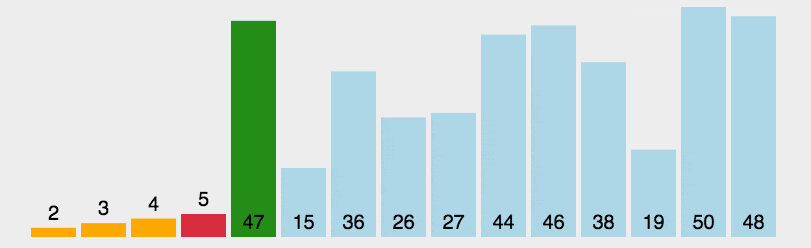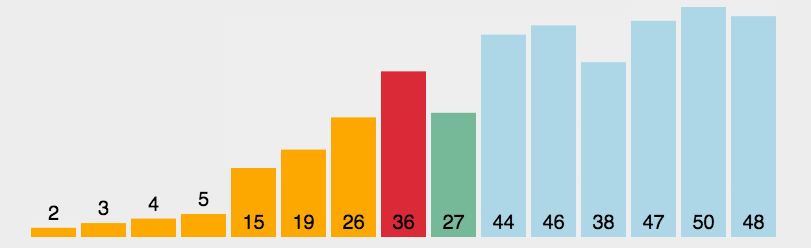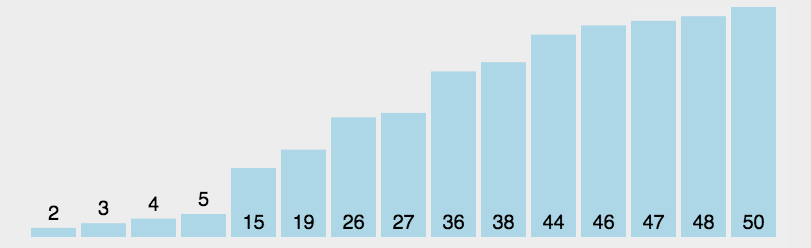
0 总览
1 冒泡排序
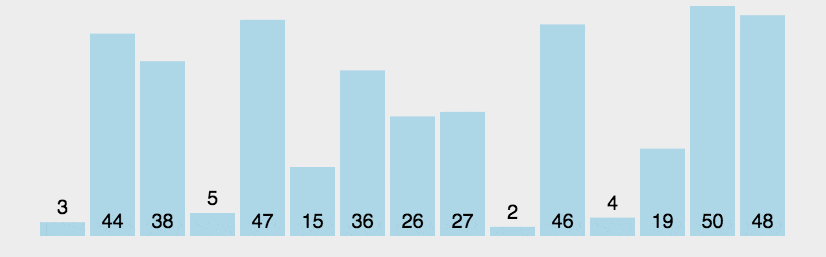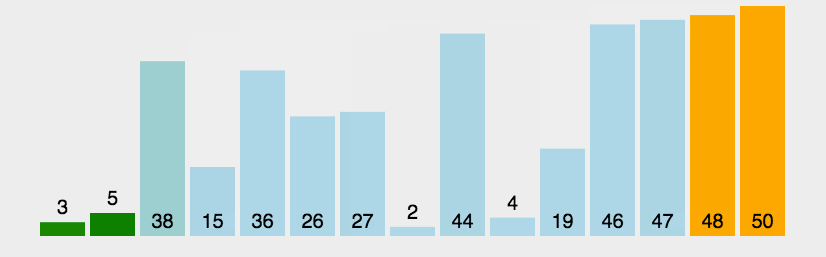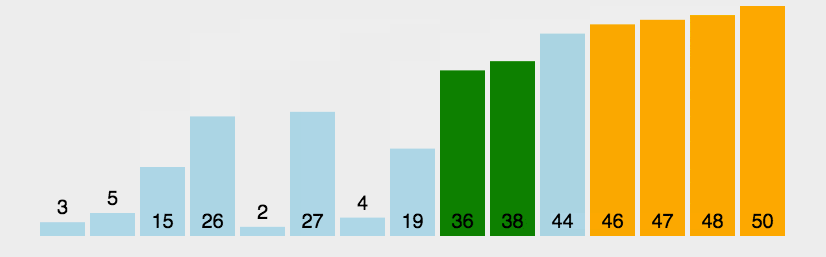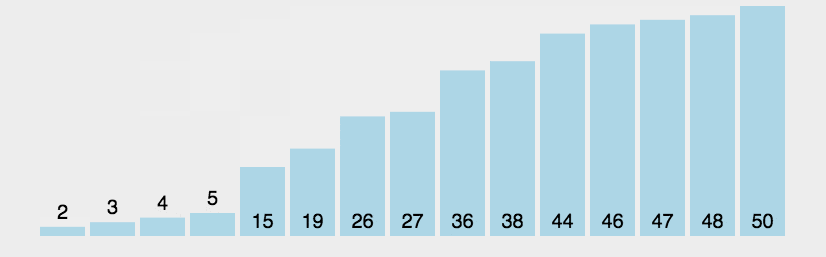
/**
* 冒泡排序
* note1: 一共循环 l.length 次
* note2: 每次循环,都把最大的放到最后
*/
public int[] bubbleSort(int[] l) {
for (int i = 0; i < l.length; i++) {
for (int j = 0; j < l.length - 1 - i; j++) { // 这里 -i 是优化
if (l[j] > l[j + 1]) {
int temp = l[j];
l[j] = l[j + 1];
l[j + 1] = temp;
}
}
}
return l;
}
2 选择排序
/**
* 选择排序
* note1: 每次选择最小的根“第一个”交换
*/
public int[] selectSort(int[] l) {
for (int i = 0; i < l.length; i++) {
int minIndex = i;
int min = l[i];
for (int j = i; j < l.length; j++) {
if (l[j] < min) {
min = l[j];
minIndex = j;
}
}
int temp = l[i];
l[i] = l[minIndex];
l[minIndex] = temp;
}
return l;
}
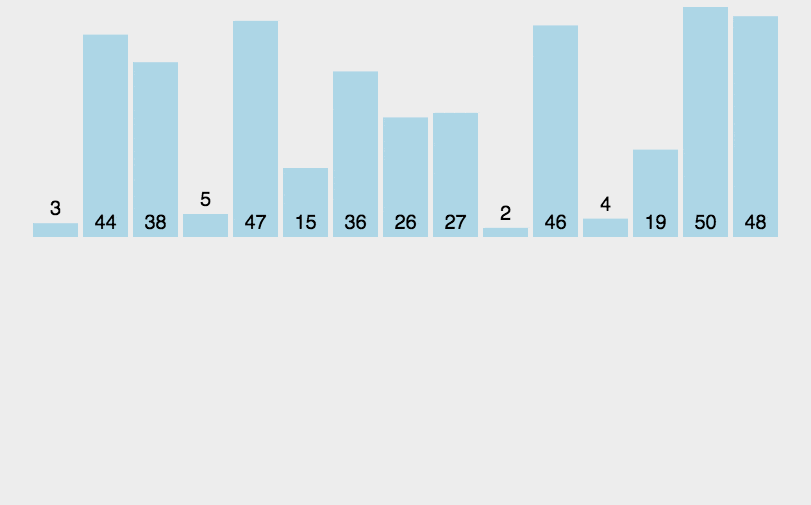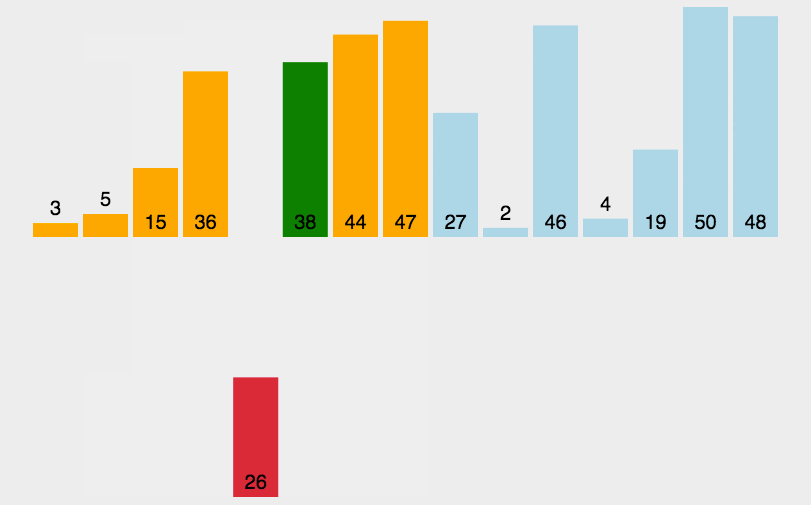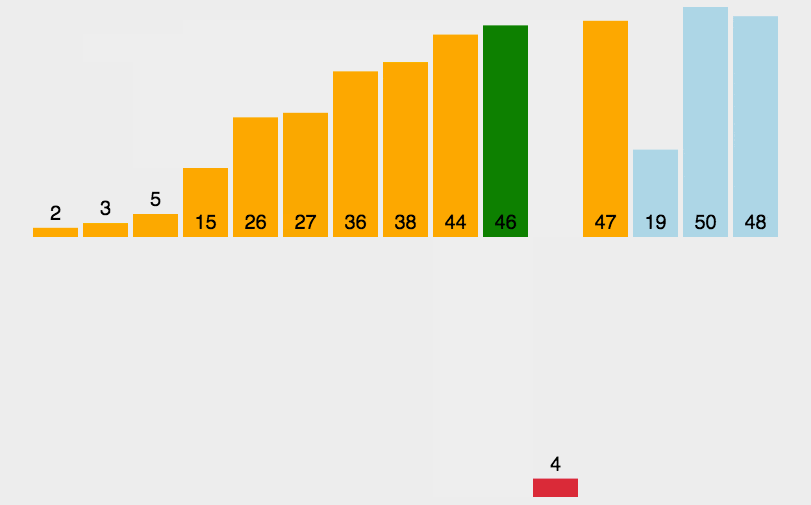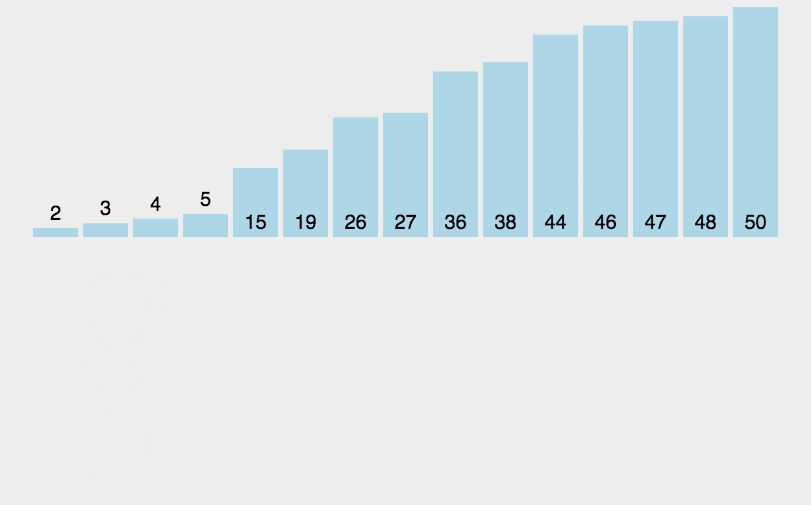
3 插入排序
/**
* 插入排序
* note1: 从后往前扫码
* note2: 把扫码到的数据,插入到现有有序列表里面
*/
public int[] insertSort(int[] l) {
// 选一个未排序的数据
for (int i = 1; i < l.length; i++) {
// 往已经排序的列表里面插入
for (int j = i; j > 0; j--) {
if (l[j] < l[j - 1]) {
swap(l, j - 1, j);
}
}
}
return l;
}
4 希尔排序
/**
* 希尔排序
* note1: 步长缩减
* note2: 插入排序
*/
public int[] shellSort(int[] l) {
for (int step = l.length / 2; step >= 1; step /= 2) {
for (int i = step; i < l.length; i++) {
int temp = l[i];
int j = i - step;
while (j >= 0 && l[j] > temp) {
l[j + step] = l[j];
j -= step;
}
l[j + step] = temp;
}
}
return l;
}
5 归并排序
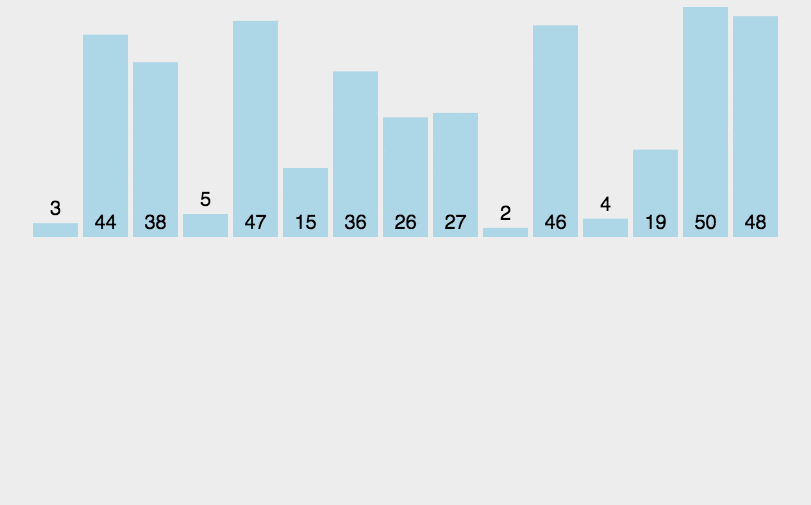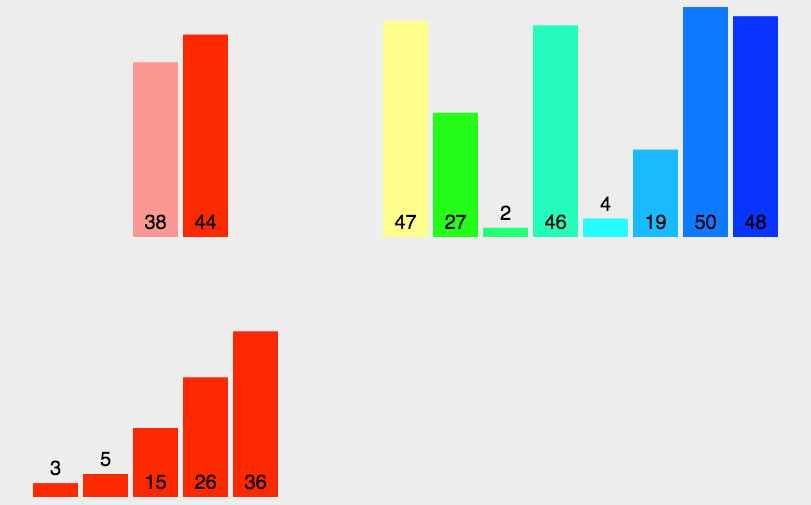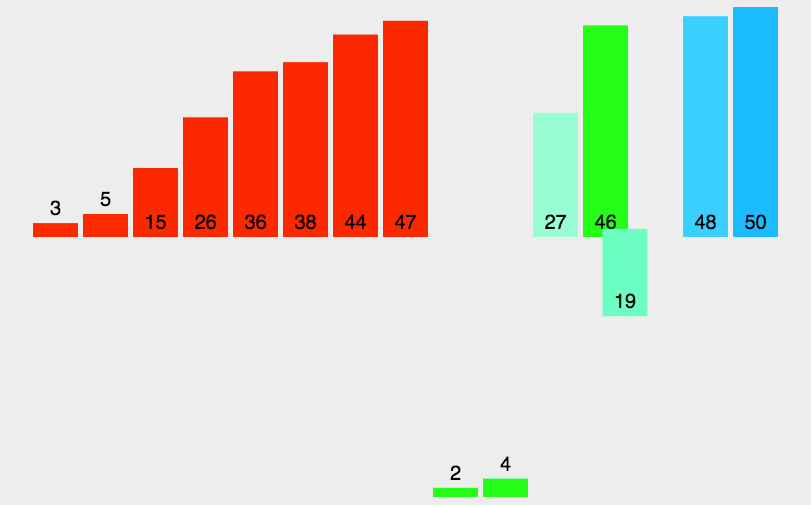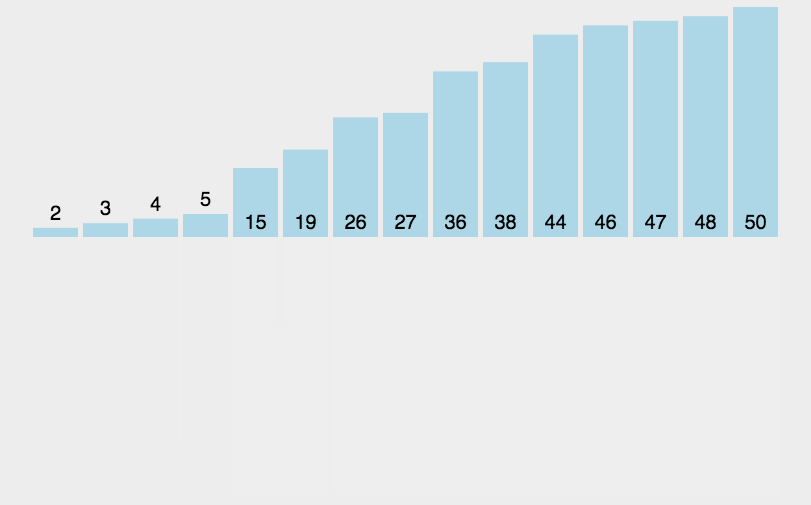
/**
* 归并排序
* note1: 分裂
* note2: 合并
* note3: 递归
*/
public int[] mergeSort(int[] l) {
if (l.length <= 1) {
return l;
}
int[] left = Arrays.copyOfRange(l, 0, l.length / 2);
int[] right = Arrays.copyOfRange(l, l.length / 2, l.length);
left = mergeSort(left);
right = mergeSort(right);
int leftIndex = 0;
int rightIndex = 0;
int lIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] <= right[rightIndex]) {
l[lIndex] = left[leftIndex];
leftIndex++;
} else {
l[lIndex] = right[rightIndex];
rightIndex++;
}
lIndex++;
}
if (leftIndex >= left.length) {
while (rightIndex < right.length) {
l[lIndex] = right[rightIndex];
rightIndex++;
lIndex++;
}
}
if (rightIndex >= right.length) {
while (leftIndex < left.length) {
l[lIndex] = left[leftIndex];
leftIndex++;
lIndex++;
}
}
return l;
}
6 快速排序
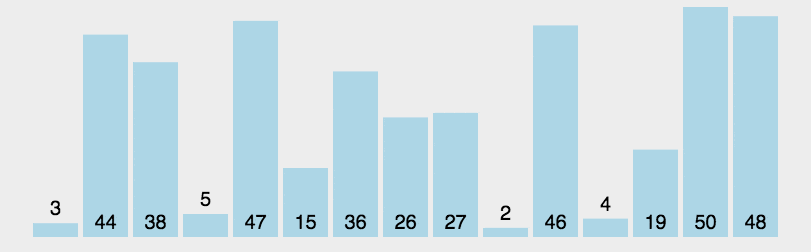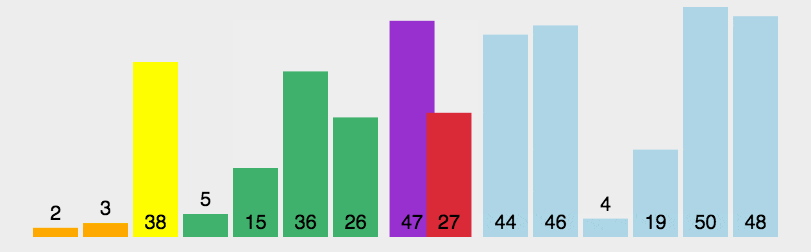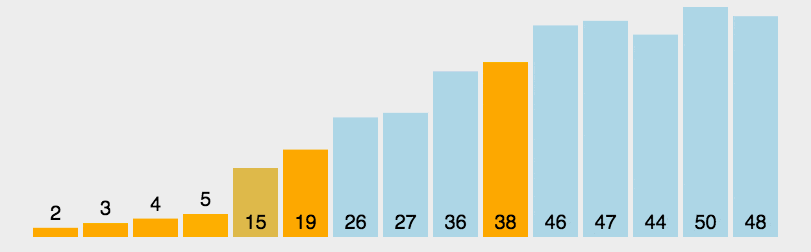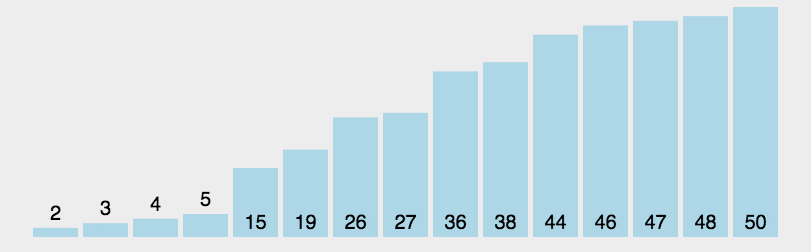
/**
* 快速排序
* note1: 选一个基准值 partition
* note2: 在递归处理基准值左面的和基准值右面的
*/
public int[] quickSort(int[] l) {
quickSort(l, 0, l.length - 1);
return l;
}
private void quickSort(int[] l, int start, int end) {
if (end - start <= 1) {
return;
}
int mid = partition(l, start, end);
quickSort(l, start, mid - 1);
quickSort(l, mid + 1, end);
}
private int partition(int[] l, int start, int end) {
int index = start + 1;
for (int i = index; i <= end; i++) {
if (l[i] < l[start]) {
swap(l, i, index);
index++;
}
}
swap(l, start, index - 1);
return index;
}
7 堆排序

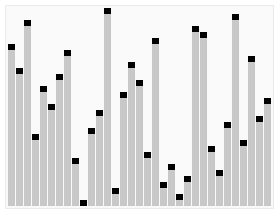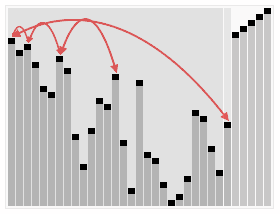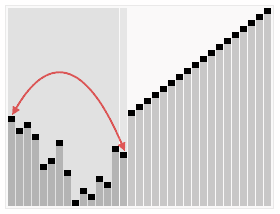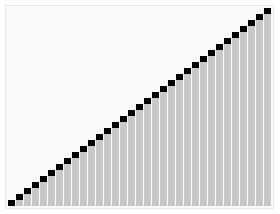
/**
* 堆排序
*/
public int[] heapSort(int[] l) {
// 构建大顶堆
buildMaxHeap(l);
int len = l.length;
for (int i = len - 1; i > 0; i--) {
swap(l, 0, i);
len--;
heapify(l, 0, len);
}
return l;
}
private void buildMaxHeap(int[] l) {
for (int i = l.length / 2; i >= 0; i--) {
heapify(l, i, l.length);
}
}
private void heapify(int[] l, int i, int len) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
if (left < len && l[left] > l[largest]) {
largest = left;
}
if (right < len && l[right] > l[largest]) {
largest = right;
}
if (largest != i) {
swap(l, largest, i);
heapify(l, largest, len);
}
}
public void swap(int[] l, int a, int b) {
int temp = l[a];
l[a] = l[b];
l[b] = temp;
}